すり替え法

この記事では、Account Thinking^🄬で扱う思考ツール「すり替え法」を紹介します。

概要

すり替え法

「すり替え法」は、難題をまず簡単な問題にすり変え、間接的に解を求める思考法です。

その特徴は「未知」を解析できることです。

にゃむーん

方程式思考の応用版です。

用法

命題を用意する

まずは、命題を用意します。

命題の例：わたしは、何のために生きるのか？

簡単な副命題にすり換える

次に、副命題にすり替えます。

副命題の例：わたしは、何のために山に登るのか？

副命題を解く

そのあと、副命題を解きます。

副命題の解の例：そこに山があるからだ。

副命題の解から、命題の解を求める

最後に副命題の解を手掛かりにして、命題の解を求めます。

命題の解の例：そこに人生があるからだ。

なかなか、カッコイイ結論が出たな。

わるたん

事例

使える人・使えない人

20代のころ、わたしには随分悩みました。

にゃむーん

「使える人」とは、いったいどのような人なのでしょう？

「じゃあ結局「使える」って何なんですか？」

• 命題　　　：　「使える人」とはどのような人か？
• 副命題　　：　「企業にとって、利用価値のある人」とはどのような人か？
• 副命題の解：　低賃金でも文句を言わない人。使い捨てにできる人。
• 命題の解　：　この発想の延長線上に求める解はない。

にゃむーん

ああ、そういうことか・・・。

この発想は、最初から間違ってたんだにゃ！

「そんな・・・小川さんの経験にはまだ利用価値が・・・」
「やべっ」（ふっ）

すり替え法の誕生秘話

20代のころ、わたしには随分悩んだ時期がありました。

にゃむーん

わたしは、何のために生きていくのだろう？

そこで、とりあえず山に登ってみました。

なんでやねん。

わるたん

にゃむーん

山に登れば何か分かるかもしれないと思ったのです。

そうして、前項に書いたとおりにすり替え法は生まれました。

行き詰まったら体を動かす。打開の方法のひとつです。

どらん先生

歴史・背景

気づきの源（フーリエ変換による微分方程式の解法）

にゃむーん

大学で学んだ微分方程式の解法が、すり替え法の気づきの源です。

残念ながら、微分方程式は原則として解けません。

そこで、フーリエ変換／フーリエ逆変換という手法を活用します。

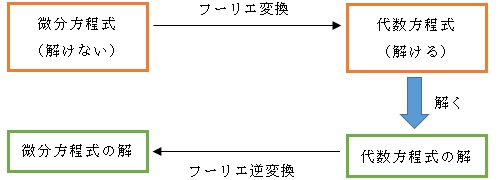
微分方程式をフーリエ変換すると、原則として解ける代数方程式に変えることができます。

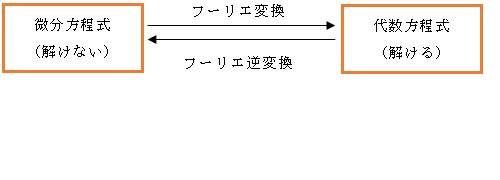
代数方程式の解をフーリエ逆変換することで、間接的に微分方程式の解を得るのです。

にゃむーん

いろいろな場面で活用できますにゃ～。

寓話の手法と似ているのです！

古代ギリシアで活躍したアイソーポスは、心理的抵抗のある問題をイソップ寓話とすることで親しみやすくしたのです！

どらん先生

まとめ

文献

引用文献

まんがでわかる7つの習慣

参考文献

「そこに山があるからだ」の元ネタについて

イソップ寓話集

応用解析要論